|
앞서 언급한 수식 (1)을 냉각탑 요구 열량 (TOWER DEMAND 또는 NUMBER
OF TRANSFER UNIT,
NTU) 이라 하며 이 식의 유도 과정은 다음과 같다.
Q = KS (hw - ha) ......(2)
여기서,
Q: 전열량, BTU/HR
K: 열 전달 계수, LB WATER/HR FT2
S: 전열 면적, FT2
hw: 냉각수 온도에서의 포화 습공기의 엔탈피, BUT/LB
ha: 습구 온도에서의 공기의 엔탈피, BTU/LB
물은 수직으로 내려 가고, 공기는
수직으로 상승하는 대향류형의 냉각탑에 있어서 물의 온도 및 공기의 엔탈피는 FILL을
따라 변하게 되기 때문에 MERKEL 관계식은 열 전달 면적의 미세 요소에 대해서
적용 될 수 있다. 즉, dQ = K (hw - ha) dS 의 관계식이 성립된다.
열 평형식 (HEAT BALANCE)으로 부터 다음 식이 유도된다.
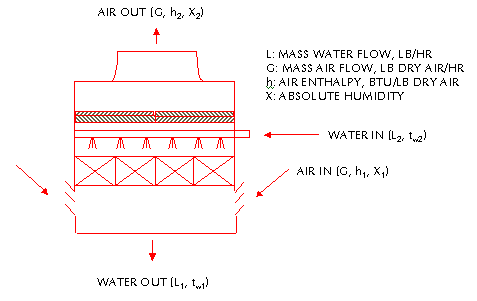
HEAT IN = HEAT OUT
....(3)
WATER IN + AIR IN = WATER OUT + AIR OUT
Cw L2 tw2 + G ha1 = Cw L1 tw1 + G ha2 .......
(4)
출구 측 수량, L1 = L2 -
G (X2 - X1)으로 증발에 의해 감소되는 양, 즉 증발 손실량 [ EVAPORATION LOSS = G (X2 - X1) ]을 뺀 것으로 이식을 상기 식 (4)에 대입하면,
Cw L2 tw2 + G ha1 =
Cw tw1 {L2 - G (X2 - X1)} + G ha2 가 되며 이 식을 정리하면,
Cw L2 (tw2 - tw1) = G ( ha2 - ha1) - Cw tw1 G
(X2 - X1) ...... (5)가 된다.
상기 식 (5)에서
MERKEL은 수리적인 계산을 간편화 하기 위하여 증발에 의한 물의 손실량을 무시하고,
즉 Cw tw1 G (X2 - X1) = 0라는 가정 하에 식 (5)는 Cw L2
(tw2 - tw1) = G ( ha2 - ha1) 관계식이 성립된다고 발표함으로써
계산의 오차를 유발하게 된 첫 원인을 제공하였다. 이 식은 다시 Cw L2 *tw
= G *ha로 표시될 수 있고 이는 어떤 지점에 있어 미소 열 전달 양 dQ와 같은
값으로, dQ = Cw L2 *tw 또는 dQ = G *ha 가 된다. 따라서 상기식을
dQ = K (hw - ha) dS 관계식에 대입하면,
Cw L2 *tw = K (hw -
ha) dS ...... (6)과
G *ha = K (hw - ha) dS ...... (7)이 얻어 지며,
식 (6)과 (7)을 적분하고 전열
면적 S 대신 S 값과 동일한 aV (a: 단위 체적 당 전열 면적, FT2/FT3,
V: 냉각탑의 유효 체적, FT3)를 사용하여 정리하면 자주 접하게
되는 아래의 식들이 구해 지게 된다.
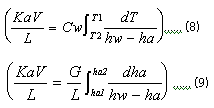
상기 식 (8)과 (9)의 우변은
명백한 무 차원이며 냉각탑에 유입되는 공기와 물의 온도만으로 계산되기 때문에 냉각탑의
크기나 FILL 형상과는 무관한 수식이다. 주어진 온도와 순환 수량에 대해 L/G는
공기 유량에 대응되는 값이며 NTU는 열 전달 요구 면적을 의미하게 된다. NTU는
L/G의 함수이며 TCHEBYCHEFF 4 지점 적분에 의해 그린 커브로 이 커브를
DEMAND CURVE라 한다. 그 이유는, 주어진 공기와 물의 온도 및 순환 수량에
대해 냉각탑이 요구하는 제거 열량을 열 전달 단위 수로 산출하는 과정이기 때문이다.
상기 수식 (9)는 다음과 같이 도표로
표현될 수 있으며, 설계 온도 조건에 대한 NTU값 계산의 시발점이 되는 것으로 매우
중요한 설계 절차 중의 하나다. 이 도표에서 AIR OPERATING LINE을 L/G라고도
하는데 이유는 Cw L (tw2 - tw1) = G ( ha2 - ha1) 관계식으로
부터 유도되는 결과를 보면 알 수 있다.
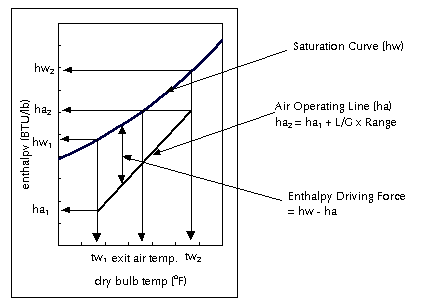
양변을 G로 나누고 정리하면, ha2
= ha1 + Cw L/G (tw2 - tw1) 이 되는데 물의 비열 Cw = 1
이고 tw2는 HWT에 해당되고 tw1은 CWT에 해당되므로 L/G 값은 직선의 기울기에
해당됨을 알 수 있다.
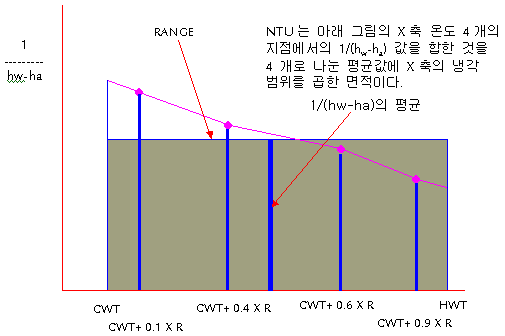
한편, 앞서 언급한 NTU 값은 어떤
한 온도에서의 물의 엔탈피로 부터 공기의 엔탈피를 뺀 즉, hw - ha의 역수를
물의 온도 CWT에서 HWT 까지 모두 합한 것이다. 이들을 적분함에 있어 계산의
간편성을 위하여 근사 적분 방식들 중의 하나인 TCHEBYCHEFF의 4 지점 적분법에
의거 4개 지점 (HWT-CWT인냉각 범위의 0.1, 0.4, 0.6 과 0.9배에
해당되는 온도) 에서의 대응되는 값인 1/hw-ha을 계산한 다음 4로 나누어 평균값을
구하고 적분 구간에 해당되는 냉각 범위를 곱한 것이 NTU에 해당 된다. 전자 계산기가>
발달한 오늘 날에도 동 방식을 이용하여 NTU 값을 계산하고 있는 이유는 계산 상의
오차가 극히 미미하기 때문이다.
다음 페이지에 계속 이어집니다. 아래의 "다음" 버턴을
누르세요...
|




