대일아쿠아

Valve positioner is a "closed loop" feedback device which receives the control signal, (usually 3-15 psi) and supply pressure up to 100 psi, receives feedback as to the blade position and adjusts the diaphragm pressure to satisfy the control signal. Valve positioners are used when air flow is critical. Control signals can be "split-ranged" to actuate the fan control using only 3-9 psi, or from 9-15 psi signal pressure.

The valve positioner receives the control air signal and outputs a higher modulated air pressure to the diaphragm which moves the fan blades to their proper position to satisfy the air flow requirements as called for by the temperature controller. For a 3 to 15 psi control signal the output pressure of the valve positioner might be 7 to 23 psi to make the fan blades moves to their required pitch angle. The advantage of the valve positioner is precise air flow control due to the feedback of blade pitch position and the ability to output high pressure on the diaphragm to quickly attain that position.

If air flow control is not critical, an "open loop" system can be used. The simplest would operate the fan using the 3-15 psi signal alone. It is an "open loop" system in that an air signal is imposed on the diaphragm and the proper pitch angel is assumed to be attained. This will be no problem for cooling towers that are not sensitive to air flow and where 15 psi diaphragm pressure is sufficient to move the blades through their required pitch travel. Operation with only 3-15 psi is generally limited to small fans.

An alternative device called a bias relay can operate most fans in lieu of a valve positioner. It is very simple, less expensive and requires no maintenance. It is mounted in the "cold" air outside the fan ring. A bias relay operates by receiving the control signal, adding or subtracting a constant pressure and multiplying the sum by a fixed gain. It outputs a modulated higher pressure to simulate the output of the valve positioner. The bias relay has to be set for a particular fan application to provide diaphragm pressure proportional to the instrument pressure to make the blades move through their desired pitch travel. Bias relays can provide the proper starting point so the blades begin decreasing pitch at 3 psi, but with a fixed multiplier or gain, they usually cannot provide the output pressure to assure an exact 12 psi span.

Another point of interest is hysteresis. There is a difference in the pitch angle versus diaphragm pressure for increasing and decreasing pressure. This is because of hysteresis in the hub operating mechanism caused by friction. Hysteresis is practically nil when a positioner is used and even if it is present and there is a slight discrepancy in air flow to control the cold water temperature, the temperature indicating controller will merely output a signal correction to meet the desired control point.

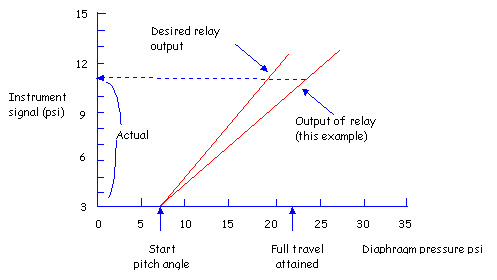
As an example, consider a fan with 20^o blade travel. This fan may require a diaphragm pressure of 7 to 23 psi to get 20^o movement from the hub. A valve positioner can achieve this exactly through its feedback mechanism. A bias relay with a bias of + 0.5 psi and gain of 2 can achieve the 7 psi diaphragm pressure with 3 psi input signal, but at 15 psi signal its output is 31 psi. The 23 psi diaphragm pressure is attained at a signal pressure of only 11 psi giving a span of 3 - 11 psi instead of 3 - 15 psi. Below figure shows this difficulty. The difficulty of obtaining an exact 12 psi instrument span is caused by the lack of choices available for the fixed multiplier (gain).

One of the most misunderstood but important characteristics of the variable pitch fan is the ability to "unload" or "feather" for minimum power consumption automatically when the ambient temperature decreases. The measurement of this no-load power condition cannot be accurately determined by the ratio method using voltage and amperage. Using this method would lead one to believe the minimum power consumption of a variable pitch fan in its feathered position would still be 30 to 50 percent of the full load. This is not true because three-phase power consumed by the motor is calculated by the relation:

HP_in = (Ampere) x (Voltage) x 1.7321 x (Power Factor) / 0.746

Without measuring power factor, accurate measurements cannot be made. Note, this would be total power consumed at "no load" fan operation. If we knew motor efficiency at no load we could calculate HP_out. No load power occurs at the "zero-flow" position of the fan pitch, usually at about minus ten degrees. This feathered mode occurs quite frequently during daytime-nighttime and summer-winter ambient temperature fluctuations and has importance in any power evaluation.

A typical case study to evaluate the direct energy saving for variable pitch fans would be prepared as follows; note that the same thermal conditions were applied to this in order to compare the fan cost differential between the fixed pitch fans and variable pitch fans.

• ●  113-89.6-80.6
• ●  4 fans (14 feet)/cell
• ●  Others remain unchanged with the previous sample design excepting using the fan ring instead of fan stack.

Below chart is to show how the blade pitch shall be varied per the changes in the airflow and air density, which results in the reduction of heat load due to the change in the ambient wet-bulb temperature. In estimating the energy comparison, the following relation is a very simple approach but a useful tool.

HP ₂ = HP _design x (CFM ₂/CFM _design)^2.8 x (Air Density ₂/Air Density _design)

Note: The air velocity at the fill was significantly reduced at the 60.8^oF of ambient wet bulb temperature reaches in case of above sample design. The normal range of air velocity in the film fill is 300 to 700 fpm. If the air velocity is less than the minimum 300 fpm at the fill, the fill efficiency will be dramatically reduced since the air shall not distributed to the entire fill evenly and the air will not be smoothly upwarded due to the less dynamic energy of air compared to the water loading.

In opposite case, that is, if the air velocity is higher than the maximum 700 fpm at the fill, all the fill efficiency shall be reduced since the contacting time of air with water droplet in the inside of fill is not enough to give the rated mass heat transfer. To avoid this condition, the water flow rate can be adjusted, some water may be bypassed, or the some fans can be stopped.

Without full automatic control, the human operator has very little incentive to be an efficient and accurate power regulator in case of two speed fan control. These have not proven very successful for the most part for lack of control discipline. Accordingly, the energy saving using variable pitch fan would be far larger than above table.