|
3) Procedure
(1) Flow: The volume (cfm)
of air delivered by the fan will be a product of the
outlet velocity as measured by the anemometer times
the area of discharge. We will arbitrarily divide the
installation types into two classes, - one where the
fan is used with no stack or a very short stack on the
outlet, and one where a relatively long stack is used.
Where a fan is used with
no stack or with an outlet stack less than 1/2 fan diameter
high above the plane of the blades, use the area of
the torus between the fan hub and cylinder or stack
as the discharge area. Divide the area of this torus
to the center of area of each. Then choose two stack
diameters at right angles to each other and take ten
readings of outlet velocity of 1/2 minute duration on
each diameter, using the intersections of the diameters
with the circles formed by the radii of equal area segments
to determine the anemometer position.
- ● Stack Height Less Than
One-Half Fan Diameter
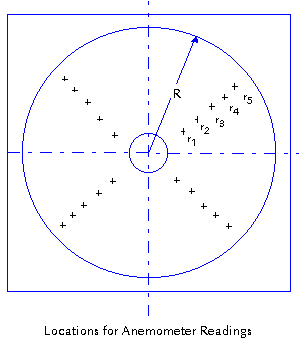
- ● Each Increment of Area
= (At - Ah) / 5
At: Total area of discharge cylinder, ft2
Ah: Area of hub, ft2
- ● Each radius for measurement
then becomes:
r1 is the radius of a circle whose area
is Ah + (At - Ah)/10
r2 is the radius of a circle whose area
is Ah + 3(At - Ah)/10
r3 is the radius of a circle whose area
is Ah + 5(At - Ah)/10
r4 is the radius of a circle whose area
is Ah + 7(At - Ah)/10
r5 is the radius of a circle whose area
is Ah + 9(At - Ah)/10
- ● Stack Height More Than
One-Half Fan Diameter
r1 = 0.316 R
r2 = 0.548 R
r3 = 0.707 R
r4 = 0.837 R
r5 = 0.948 R
Where a fan is used with
a discharge stack greater than 1/2 fan diameter high
above the plane of blades, the entire area of the inside
of the fan stack or cylinder at the plane of measurement
becomes the discharge area. Again, divide the stack
area into five equal areas and determine the radii to
the centers of area of each. Choose two stack diameters
at right angles to each other and proceed as above.
Again, the sketch in above figure will help to clarify
this procedure.
There are two methods of
using the anemometer. The discharge from the fan is
far from axial and contains varying amounts of rotation.
The angle of discharge immediately above the fan varies
from hub to tip and also varies with the pressure the
fan is working against. As the discharge stack becomes
higher, the an stream tends to lose some of this rotational
component, but usually there is some angle of yaw even
with a stack one fan diameter high and a low static
head. By placing a simple protractor on the extension
rod of the anemometer and using a light thread attached
to the anemometer housing, the angle of yaw can be determined
just before the 1/2 minute readings are taken.
The anemometer can be held
either normal to the plane of fan rotation or normal
to the flow. The correction is less tedious if the first
method is used and also depends less on the operator?
judgment so this is the method we suggest. If an accuracy
of 2% is acceptable and the yaw angles do not exceed
20o as is quite common, no correction
for yaw need be made. If higher accuracy is required
the readings can be corrected by using below table.
| Corrections
for Anemometer Held Normal to Plane of Fan Rotation |
| Yaw
Angle, Degrees |
Correction,
Percent |
| 5 |
-
0.10 |
| 10 |
-
0.5 |
| 15 |
-
1.1 |
| 20 |
-
2.0 |
| 25 |
-
3.0 |
| 30 |
-
4.0 |
| 40 |
-
5.1 |
| 50 |
-
8.2 |
After the anemometer readings
are taken for one-half minute duration they must be
doubled to obtain ft/min then corrected for anemometer
calibration, and corrected again for yaw angle. Since
these readings were all taken at the centers of area
of five equal areas, the average of the twenty corrected
readings multiplied by the fan discharge area in square
feet will give the volume of air (cfm) delivered by
the fan.
The effect of air densities
other than calibration density (0.075 lb/ft3)
is rather low, especially at the velocities found in
a cooling fan discharge. Therefore, no correction usually
is made. The toleration in density ratio for a one percent
variation in accuracy is shown in below table.
|
Toleration of Changes
in Air Density |
| Velocity
(ft/min) |
Max.
value of d/da for 1% error |
| 300 |
1.05 |
| 600 |
1.10 |
| 1200 |
1.21 |
| 1800 |
1.32 |
If desired, the average velocities
at each of the five radii can be determined from the
data. These can then be plotted against the radius to
graphically portray the fan velocity profile. This has
no bearing on the test results, but will be of interest
to the fan designer and the tower manufacturer in case
remedial action is necessary.
(2) Static Pressure: Static
pressure measurements should be taken in the plenum
beneath the fan deck in air that is a quite as possible,
and in a plane that is 6" to 12" below the
fan stack entrance. It is suggested that the 1/4"
tube be inserted through the fan deck at four points
approximately midway between the base of the fan cylinder
and the corner of the cell on the two cell diagonals
as shown in below figure.
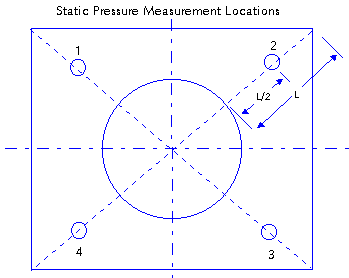
Care must be taken that the
tube end is not near an opening in a cell wall or near
a break in partition wall so that it will not be affected
by a jet or stream of high velocity air. Care must also
be taken to shield the manometer from high velocity
air currents. Remember that the magnitude of the readings
can be quite small, but will have a great effect on
the fan efficiency as will be shown later.
Readings should be taken
at each of the four locations at the beginning and the
end of the flow tests. The average of these eight readings
will be the fan static pressure. This is only true if
there are no obstructions on the fan discharge. A guard
over the fan outlet or on top of the fan stack, for
example, adds to the static head against which the fan
is working. It is extremely difficult to measure this
pressure and it is recommended that it be calculated.
Various authorities have given estimates for the resistance
of guards in terms of the average velocity pressure
in the stack. A reasonable estimate for various guards
is shown in below table.
| Guard
Material |
Resistance
% of Stack Velocity Pressure |
| 1/2"
x 14 Ga. Woven Wire Cloth |
32.0 |
| 1"
x 13 Ga. Woven Wire Cloth |
17.6 |
| 2"
x 12 Ga. Woven Wire Cloth |
9.6 |
| 1/2"
x 18 Ga. Expanded Metal |
49.6 |
| 1/2"
x 18 Ga. Expanded Metal Flattened |
75.0 |
| 1"
x 18 Ga. Expanded Metal |
27.2 |
| 1"
x 18 Ga. Expanded Metal Flattened |
41.6 |
| 1-1/2"
x 18 Ga. Expanded Metal |
19.2 |
| 1-1/2"
x 18 Ga. Expanded Metal Flattened |
22.4 |
Example: If a guard made
of 1?x 14 gage commercial expanded metal is placed over
a stack with an average velocity of 1800 fpm, the approximate
resistance pressure is: SP = (27.2/100) x (1800/4005)2
= 0.055"
Although the static pressure
on the fan discharge is positive and that on the inlet
is negative, they must be added arithmetically disregarding
the sign since they represent the entire static pressure
against which the fan is working.
(3) Air Density: From readings
of the dry bulb and wet bulb temperatures in the fan
discharge and barometric pressure reading, the density
of the air handled by the fan can be determined. Readings
should be taken at four points and averaged. Standard
tables and psychrometric chart are available, therefore
the procedure will not be given here. Note that it is
quite difficult to get extremely accurate dry bulb measurements
in the fan discharge due to the presence of so much
free water in the stream. However, the percentage error
in air density for a 1o error in dry bulb
reading is extremely small (approximately 0.2%) and
need cause no concern.
(4) Fan Speed: Most of the
units we are considering have the fan mounted on a reduction
gear driven by an electric motor. The motor rpm can
be easily measured by a tachometer. Then by rotating
the motor shaft by hand and counting the turns required
to get 10 fan revolutions, the gear ratio can be determined.
From this data and the motor speed, the fan rpm can
easily be determined. The use of belt drive complicates
this procedure slightly, since there will be some slippage
at operating speed. The best measurement for such a
case is either a revolution counter attached to the
hub or a stroboscopic device calibrated in rpm.
(5) Power: On three phase
electrical installations, the motor input horsepower
can be calculated as follows:
HP(input) = (Volts
x Amperes x 31/2 x Power Factor) / 746 =
Watts / 746
In order to determine the
brake horsepower absorbed by the fan, it is necessary
to know the motor and gear efficiency. This can be taken
from the manufacturer? curves with very good accuracy.
The fan horsepower then is: bhp fan = (hpinput)
x Efficiency of Gear x (Efficiency of Motor).
Usually motor efficiency
curves are not reliable when the operating voltage varies
greater than +/- 10% of the motor nameplate.
4) Calculation of Fan Performance
We now have a set of values
for flow (cfm), static pressure (sp) and fan brake horsepower
(bhp) under the density conditions existing at the fan
outlet. In order to relate these to the curve of the
fan made from wind tunnel tests, we must convert these
values to standard air with a density of 0.075 lb/ft3.
This is very simple. The air flow (cfm) needs no conversion
since the fan is a constant volume machine and the volume
moved does not vary with density. The static pressure
(sp), and brake horsepower (bhp), however, do vary directly
as the density. The conversion then becomes:
- ● cfm (standard air) = cfm
- ● sp (standard air) = sp
x (0.075 / test density)
- ● bhp (standard air) = bhp
x (0.075 / test density)
In order to calculate the
total efficiency of the fan, we must calculate the velocity
head (vp) and add it tothe static head. We do this knowing
the area of the fan stack. The formula is: vp = [cfm
/ (A x 4008.7)]2, where A is area of inside
of fan stack at the plane of the fan.
Please note again that although
the velocity pressure is positive and the static pressure
is negative, they are added arithmetically disregarding
the sings. tp = sp + vp, tp = total pressure. We now
have all the factors in standard air to calculate the
fan total efficiency.
Total Efficiency = (cfm x
tp)/(6356 x bhp)
We can now plot this one
point on the fan curve from the tunnel test to check
the relation. Generally, the field test points falls
very near the test curve. On a combining factor of flow,
pressure and brake horsepower, the field tests generally
come within +/- 5% of the fan curve. Certainly this
test method is a far cry from laboratory testing, but
there are various factors that lead to this in addition
to the obvious errors in the test method. Many times
the fans are not tested with the proper AMCA type test.
Experience indicates that if a fan is tested in accordance
with AMCA Bulletin #210 using the chamber test set-up
type B with outlet duct, then the field test and the
tunnel test will line up very well.
Another factor that influences
the performance of the fan is the effect of the drift
eliminators in the towers. If these are less than 1/2
fan diameter away from the fan entrance, they can act
as partial intake guide vanes either turning the air
to effect an apparent increase or decrease in fan angle.
This can very easily be the guide vane effect of the
drift eliminators.
Another important factor
in fan performance is the tip clearance of the blades.
Excessive tip clearance becomes more and more of a factor
as the resistance of the tower increases. This can completely
throw out any correlation between field and tunnel testing.
In one recent test tip clearance on a 6?fan was 1/2"
too great. The cylinder was lined with fiber board,
and the test was re-run, showing an increase of about
18% in fan efficiency. Lastly, the entrance used to
the fan should be the same type as you do from a smooth
bell entrance. The difference may amount to as much
as 0.4vp added to the fan as effective static pressure.
A question that often arises
is: ?ow much increase in air flow can be obtained by
a given increase in fan horsepower??In other words,
if more air is desired on a given tower with a constant
fan speed, the fan blade angle can be changed and absorb
more power. If the fan efficiency would remain constant,
the change in flow would be directly proportional to
the cube root of the horsepower ratio. Unfortunately,
the fan total efficiency varies from free air to block-off,
and also varies with blade angle. Strictly speaking,
there is no hard and fast rule for this. However, it
would be safe to apply this rule for variations in horsepower
not to exceed 15% so long as the fan was originally
operating well back from a stall point. The fan manufacturer
should be consulted for his recommendations in such
cases. There have been cases where the flow actually
dropped when the angle was increased although the power
absorbed by the fan increased. In this case, the increase
in angle put the fan into the stall range.
If the change in horsepower
can be effected by a change in fan speed only, the only
limiting factor is the tip-speed limitation of the fan.
You would not likely reach any critical section speeds
in general applications. In this case, the flow would
definitely vary as the cube root of the horsepower ratio.
|


